Statistical Methods III: Week-6

Case Study: The Challenger Disaster

1. Events and Main Points

• Jan 27, 1986 (Night before the launch):
  • A 3-hour teleconference was held between:
    • Morton Thiokol (manufacturer of the solid rocket motor)
    • Marshall Space Flight Center (NASA design control)
    • Kennedy Space Center
  • Main topic: Effect of 31°F forecast temperature on O-ring performance
• Data Presented (Figure 1a):
  • Each point = a shuttle flight with O-ring thermal distress
  • X-axis = joint temperature, Y-axis = number of distressed O-rings
  • Zero-failure flights were omitted, making the plot misleading
  • From this “U-shaped” plot, some concluded there was no clear temperature effect
• Debate During Teleconference:
  • Some recommended delaying launch until temperature was above 53°F, the lowest prior launch temperature (which had the most O-ring distress)
  • Others believed data was inconclusive, though physical evidence suggested otherwise
  • Roger Boisjoly (Thiokol engineer) insisted that temperature was a discriminator
• Final Recommendation by Morton Thiokol:
  • Proceed with launch
  • Stated: “Temperature data [are] not conclusive on predicting primary O-ring blowby.”
  • Acknowledged colder O-rings become harder, take longer to seat, and thus are riskier
• Jan 28, 1986 (Launch Day):
  • Challenger launched at 31°F
  • Catastrophic failure occurred shortly after liftoff due to O-ring seal breach
• Aftermath – Rogers Commission Findings:
  • Cause: Combustion gas leak through the right booster aft field joint
  • Determined that the key analysis mistake was excluding zero-incident flights from the plot
  • Including them shows a clear correlation between low temperature and O-ring failure
  • Concluded that proper statistical analysis would have revealed the danger

The Challenger disaster underscores how flawed data visualization and the exclusion of critical information (zero-incident flights) led to a catastrophic decision. Proper statistical reasoning could have prevented the tragedy.

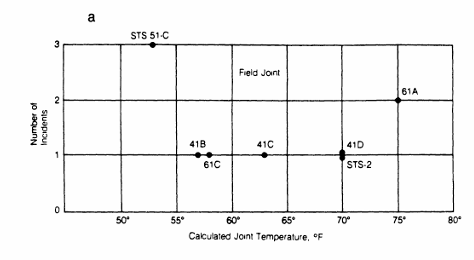
Figure 1a: Visualization excluding zero-incident flights.

Figure 1b: Correct visualization including zero-incident flights.

Main Points and Events

• Section 3 – Evidence of Temperature Effect
  • Analysis of O-ring thermal-distress data shows strong statistical evidence that temperature affects O-ring performance.
  • This alone could have influenced the teleconference decision before Challenger’s launch.
• Section 5 – Probabilistic Risk Assessment
  • Using Section 3’s analysis as a base, a risk assessment was done for catastrophic O-ring failure.
  • Under Challenger’s actual launch conditions (31°F): Probability of failure ≥ 13%.
  • If postponed to 60°F: Probability of failure ≥ 2%.
• Section 5.2 – Uncertainty in Estimates
  • A postanalysis prior distribution was derived for future risk assessment.
  • At 31°F: mean probability ≥ 16%, median ≥ 13%.
  • At 60°F: mean probability ≥ 0.004, median ≥ 0.02.
• Additional Analyses (Sections 4 & 5)
  • Studied other factors:
    • (a) Nozzle-joint O-ring performance (important since nozzle and field joints use the same type of O-ring)
    • (b) Leak-check pressure effects
    • (c) Influential observations
    • (d) Possible model misfit
• Connection to NASA Reforms
  • Some work was conducted while Bruce Hoadley served on the Shuttle Criticality Review Hazard Analysis Audit Committee (SCRHAAC).
  • Recommendations from SCRHAAC (1988), influenced by this analysis, received press attention and changed NASA practices.
  • NASA began:
    • Building a staff skilled in statistical science
    • Conducting probabilistic risk assessments of major subsystems
• Purpose of Article
  • Intended as a blueprint for future NASA risk analyses.

These sections emphasize how statistical analysis revealed the strong role of temperature in O-ring failure, provided probabilistic risk estimates under varying conditions, and ultimately influenced NASA’s reforms toward systematic probabilistic risk assessment.

Main Points and Events

2. Shuttle System

• Shuttle consists of 4 subsystems:
  • Orbiter (crew + controls)
  • External liquid-fuel tank (feeds orbiter’s main engines)
  • Solid rocket motors (made by Morton Thiokol)
• Focus: Solid rocket motors because the Challenger accident was caused by O-ring failure at motor field joints
• Motors are shipped in 4 pieces and assembled at Kennedy; joints = field joints
• Similar joint with nozzle = nozzle joint
• O-rings:
  • Two per joint (primary + secondary)
  • 37.5 ft diameter, 0.28 in thick
  • Designed to seal gaps between metal casings

O-ring Function & Issues

• At ignition: pressure + heat build → O-rings erode
• Putty used to protect O-rings; pressure displaces putty → pressurizes behind O-ring → energizes seal
• Leak test port added; pressure test raised from 50 → 100 → 200 psi
• Engine qualified to 40°F minimum operating temperature

Early Evidence of Problems (Pre-1986)

• 1977: NASA discovered field-joint rotation → casings bulge → tang rotates relative to clevis → joint gap widens
  • Primary O-ring usually seals
  • Secondary O-ring can lose contact → no redundancy
  • Memos (1978–79): design change “mandatory” to prevent catastrophic failure
• 1982: Secondary O-rings officially classified as non-redundant

Shuttle Flights Evidence

• 1981 onward: Thermal distress observed in O-rings
  • Erosion: heat burns O-ring
  • Blowby: hot gases leak past O-ring
  • Blow holes in putty (exacerbated by higher test pressures) suspected
• Engineering models predicted max erosion depth = 0.09 inches

Key Flights

• Jan 24, 1985 (Flight 51-C, at 53°F):
  • Severe erosion + blowby in primary O-ring, erosion in secondary O-ring
  • Review acknowledged: “low temperature enhances blowby probability … condition not desirable but acceptable”
• Apr 29, 1985 (Flight 51-B, at 75°F):
  • Nozzle-joint primary O-ring eroded 0.171 inches → never sealed
  • Secondary eroded 0.032 inches
  • Memo: “If same scenario in field joint … result would be catastrophe”
• June 1985 – Bench test of O-ring resiliency:
  • At 100°F: O-ring maintained contact after joint rotation
  • At 50°F: O-ring failed to reestablish contact
  • Commission conclusion: O-ring resiliency directly related to temperature. Warm O-rings reseal faster; cold O-rings may not seal at all
• Aug 1985 NASA briefing:
  • Stated “qualitative probability of secondary O-ring failure is high” if erosion penetration occurs after ~330 ms of ignition

Atmosphere Before Challenger Launch

• By Jan 1986, ample evidence existed:
  • Field-joint rotation risk
  • O-ring thermal distress (erosion + blowby)
  • Low temperatures significantly worsened performance
• Teleconference discussions occurred under serious doubts about O-ring reliability in cold conditions

⚠️ Core takeaway: Before Challenger, both engineering tests and past flights showed strong warnings about O-ring vulnerability, especially at low temperatures. These warnings were known to NASA and Thiokol well before Jan 1986.

🚀 Section 3: Data Analysis for Field-Joint O-Rings

3.1 Model Fitting

Data Setup

• We have 23 shuttle flights with thermal distress data
• Each flight has 6 primary O-rings
• Outcome: number of O-rings showing thermal distress (erosion or blowby)
• Secondary O-rings: only 1 case of damage, so ignored in modeling

Modeling Framework

• Let X = number of distressed O-rings in a flight
• Assume Binomial distribution with probability depending on:
  • Temperature at launch (t)
  • Leak-check pressure (s)
  • Probability of damage per O-ring: p(t,s)
• Logistic regression with temperature + pressure:
  • Intercept: α̂ = 2.52
  • Temperature effect: β̂ = -0.0983 (negative → higher temp = less damage)
  • Pressure effect: γ̂ = 0.00848 (very weak)
• Goodness of fit: G² = 16.546 (20 df) → good fit

Dropping Pressure

• Pressure effect not statistically significant
• Temperature-only model:
  • α̂ = 5.085
  • β̂ = -0.1156
• G² = 18.086 (21 df) → also good fit
• Conclusion: Temperature is the key predictor

Visualization (described)

• At ~30–40°F: predicted ~4–5 of 6 O-rings distressed
• At >70°F: predicted ~0 O-rings distressed

Alternative Binary Model

• Defined binary outcome: 1 if ≥1 O-ring incident, 0 otherwise
• Logistic regression (temperature-only) → results similar to binomial model
• Interpretation: low temperature = high risk

3.2 Confidence Intervals

• Method: parametric bootstrap (Efron 1979)
• Findings:
  • At low temps (<65°F): intervals wide (high uncertainty)
  • At high temps (>65°F): intervals narrow (more stable)
  • At 30°F: expected # incidents ~1 to 6 O-rings (uncertain but clearly dangerous)

3.3 Effect of Data Perturbations

• Sensitivity analysis: remove each flight one by one
• Key result: Flight 21 (75°F, 2 incidents) was highly influential
  • Removing it shifted coefficients ~4 SDs
  • Probability of such an event under model < 0.001
  • But it was real → suggests unmodeled factors
• Even without Flight 21 → low temperature risk remains very high

🔑 Key Takeaways from Section 3

• Temperature is dominant factor; pressure negligible
• Logistic regression confirms: ~31°F → majority of O-rings expected to fail
• Uncertainty large at very low temps, but always points to high risk
• Flight 21 anomaly shows model is imperfect but doesn’t change conclusion
• Statistical evidence strongly supported engineers’ warnings before Challenger

🔎 3.4 The Form of the Model — Detailed Summary

Why check the form?

• Logistic model assumes:
  • Logit link is correct
  • Logit(probability) vs temperature is linear
• With only 23 points, authors preferred simplicity but tested linearity assumption

Testing Quadratic Term

• Quadratic term γ̂ = 0.0041 (not significant)
• Likelihood ratio = 0.494 (df=1), far below threshold
• No evidence of curvature → straight line is adequate

Nonparametric Smoothing Check

• Used Cleveland & Devlin (1988) smoothing with f = 0.4
• Smoothed curve ≈ logistic fit
• Conclusion: linear logistic model fits well

Residual Diagnostics

• Checked standardized residuals
• Outliers:
  • Point 9 (smoothed = 0)
  • Point 21 (anomalous influential flight)
• Otherwise: no evidence of systematic nonlinearity

Local Deviance Plots

• Compared local vs global deviance
• Fit adequate except large jump between points 14 & 15 (due to Flight 21)
• Removing Flight 21 → diagnostics still support adequacy

ACE Algorithm

• ACE (Breiman & Friedman 1985) checked transformations
• Found logit(probs) vs temperature ≈ linear
• Strong evidence logit link is appropriate

Pressure Variable Diagnostics

• Re-introducing pressure failed:
  • Very few data points
  • Only one case with incident at 50 psi
  • Smoothing unreliable, Newton-Raphson unstable
• Conclusion: pressure cannot be modeled reliably

🔑 Final Takeaways from Section 3.4

• Linear logistic model (temperature-only) is adequate
• Nonparametric smoothing, residuals, and deviance checks confirm adequacy (except Flight 21)
• Logit link is appropriate, simpler and stable
• Pressure variable discarded as unreliable

👉 Bottom line: The Challenger O-ring data strongly supported a simple, linear logistic regression of failure probability vs temperature. The model was statistically sound, stable, and showed clear risk at low temperatures, despite one influential anomaly.